Bloomberg

Interview

Merge Two Sorted Lists, LeetCode OJ

Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists. ( Source: LeetCode OJ )

Merge Two Sorted Lists, Solutions

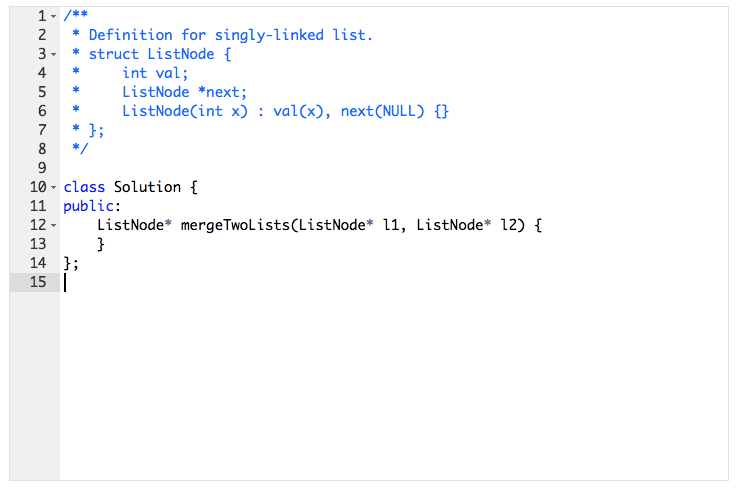
Solution #1: Classic STL Solution, Immutable parameters

The following image is a snap shot of the solution developed using the Xcode 7.2.1 IDE and the results given by LeetCode OJ:

Right-click and "Save Image as ..." to get a better look at this image!

When first looking at this problem I wondered if it would be possible to simply iterate down each of the link lists and make the appropriate connections based on the links already established in the list. Within a very short amount of time I realized that this is precisely what the STL framework was meant to address. So I quickly changed everything in light of a typical STL application for a problem such as this. One thing I overlooked in this task was that the lists to be merged were already sorted. I mistakenly assumed that they were not going to be sorted and developed a solution that sorted the lists from inside the method. Turns out I ended up hitting two birds with one stone, this is typical of applications written using STL in my experience. Within an hour I had a most elegant solution based on the STL framework:

// Solution #1

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

std::list<int> intList;

ListNode* h1 = l1, *h2 = l2;

while ( h1!=NULL ) {

intList.push_back(h1->val);

h1 = h1->next;

}

while ( h2!=NULL ) {

intList.push_back(h2->val);

h2 = h2->next;

}

ListNode* listNode = new ListNode(0), *p = listNode, *result = listNode;

intList.sort();

std::list<int>::const_iterator iterator;

for (iterator = intList.begin(); iterator != intList.end(); ++iterator) {

int value = *iterator;

p = listNode;

listNode->val = value;

listNode = new ListNode(0);

p->next = listNode;

}

p->next = NULL;

if ( p == listNode ) {

delete listNode;

return NULL;

}

return result;

}

};

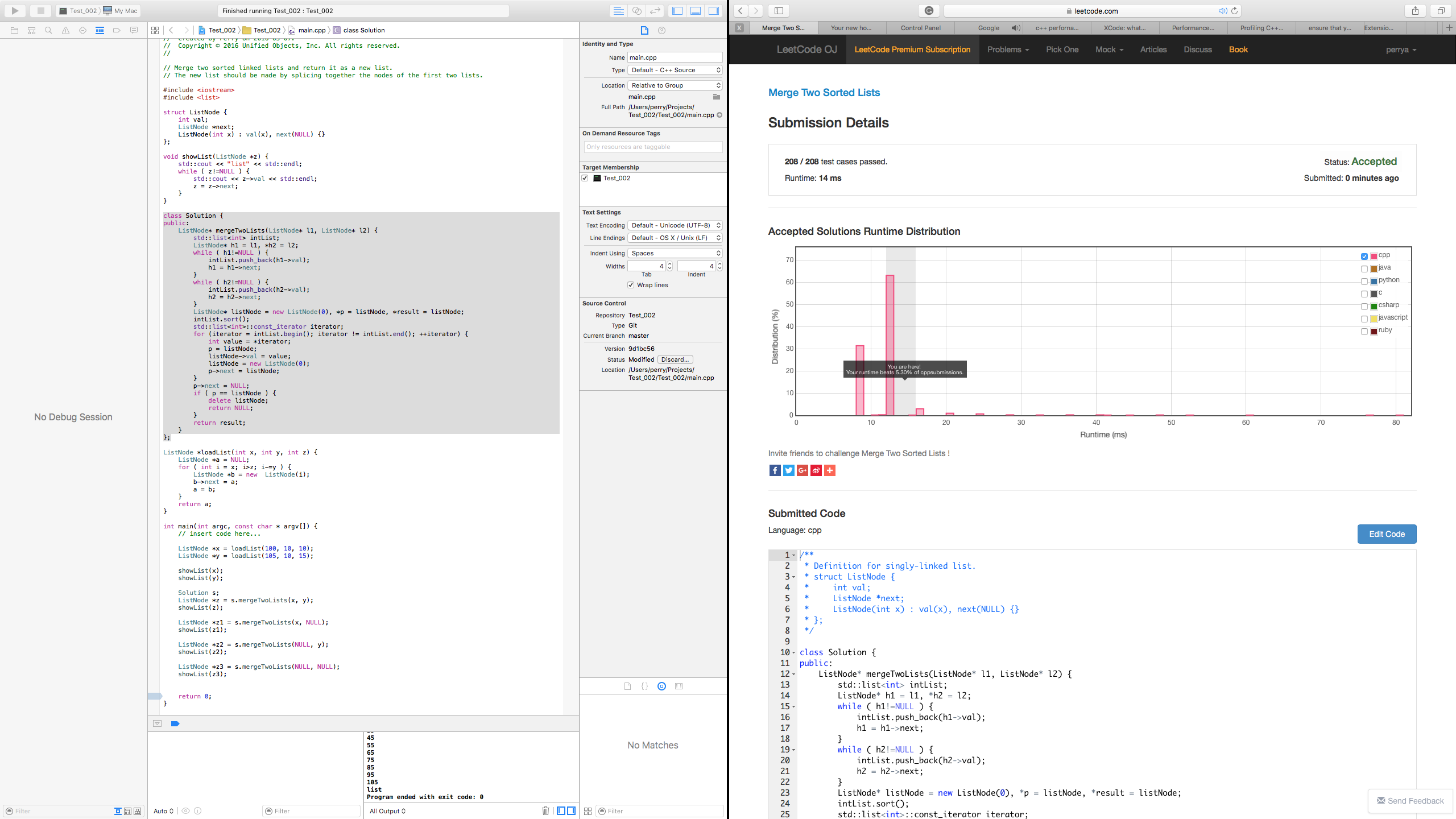
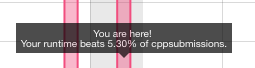
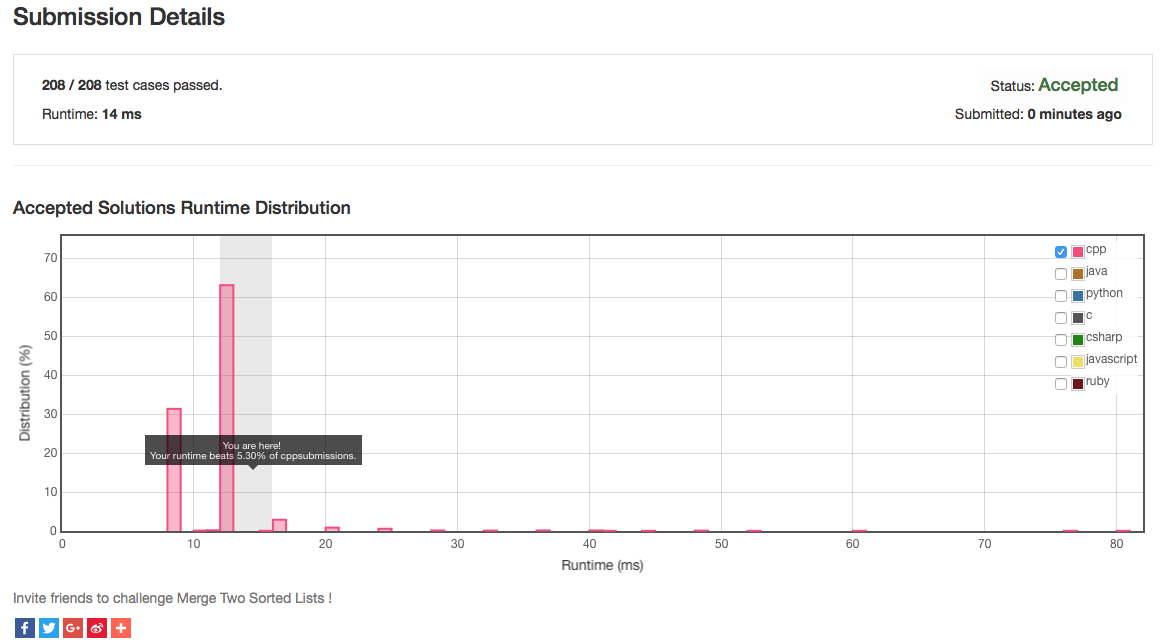
Essentially what we do is read the values of both linked lists an place them inside an STL list container. From there we merely do a simply sort of int values before creating a new link list containing the sorted values to be passed back to the client. Here we make use of the typical STL container classes such as std::list and for transversing the list we use the classic STL iterator. The standard built-in STL list.sort() utilizes it's default sorting algorithm.

When I submitted my solution to the LeetCode OJ database for approval I was rather surprised to see a graph comparing my results with many others. Unfortunately for me I misread the rating on the report that suggested that my solution may not be the most efficient:

I was further confused by the layout of the graph that seemed to suggest that some people were able to submit a solution many, many times faster than mine. Curious as to how I could improve on my simple and elegant STL solution I decided to alter the solution to make use of classic optimizations often associated with C/C++ performance and memory issues.

Right-click and "Save Image as ..." to get a better look at this image!

Based on what I was reading from the above graph I became so curious as to how I could make my solution much more efficient. In this LeetCode OJ example it is merely a case of merging two link lists but in real world C++ applications it might be a situation where performance and resources become an issue. With over 320,000 total submissions and over 110,000 total accepted solutions, I wanted to know if what I was reading from the graph was accurate seeing how I basically applying STL in a classic manner to address this problem. I really wanted to know if a standard STL solution was going to be adequate or if a more generic approach could produce better results. So I decided to apply techniques that I learned from previous real world C++ application development to see if I could improve my rating.

Solution #2: Classic Heap Sort Solution, Immutable parameters

The following image is a snap shot of the 2nd solution developed and the results given by LeetCode OJ:

Right-click and "Save Image as ..." to get a better look at this image!

My second solution to this problem didn't take all that long to do compared to my first attempt to come up with a solution, perhaps a mere 1/2 hour at most. Here, I simply remove all references to the STL framework and in it's place put in a classic heap sort solution based on arrays:

// Solution #2

void MAX_HEAPIFY(int a[], int i, int n)

{

int l,r,largest,loc;

l=2*i;

r=(2*i+1);

if((l<=n)&&a[l]>a[i])

largest=l;

else

largest=i;

if((r<=n)&&(a[r]>a[largest]))

largest=r;

if(largest!=i)

{

loc=a[i];

a[i]=a[largest];

a[largest]=loc;

MAX_HEAPIFY(a, largest,n);

}

void BUILD_MAX_HEAP(int a[], int n)

{

for(int k = n/2; k >= 1; k--)

{

MAX_HEAPIFY(a, k, n);

}

void HEAPSORT(int a[], int n)

{

BUILD_MAX_HEAP(a,n);

int i, temp;

for (i = n; i >= 2; i--)

{

temp = a[i];

a[i] = a[1];

a[1] = temp;

MAX_HEAPIFY(a, 1, i - 1);

}

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

ListNode* h1 = l1, *h2 = l2;

int n = 0;

while ( h1!=NULL ) {

n++;

h1 = h1->next;

}

while ( h2!=NULL ) {

n++;

h2 = h2->next;

}

h1 = l1, h2 = l2;

int a[n], i=1;

while ( h1!=NULL ) {

a[i++] = h1->val;

h1 = h1->next;

}

while ( h2!=NULL ) {

a[i++] = h2->val;

h2 = h2->next;

}

HEAPSORT(a, n);

ListNode* listNode = new ListNode(0), *p = listNode, *result = listNode;

for (int i = 1; i <= n; i++) {

int value = a[i];

p = listNode;

listNode->val = value;

listNode = new ListNode(0);

p->next = listNode;

}

p->next = NULL;

if ( p == listNode ) {

delete listNode;

return NULL;

}

return result;

}

};

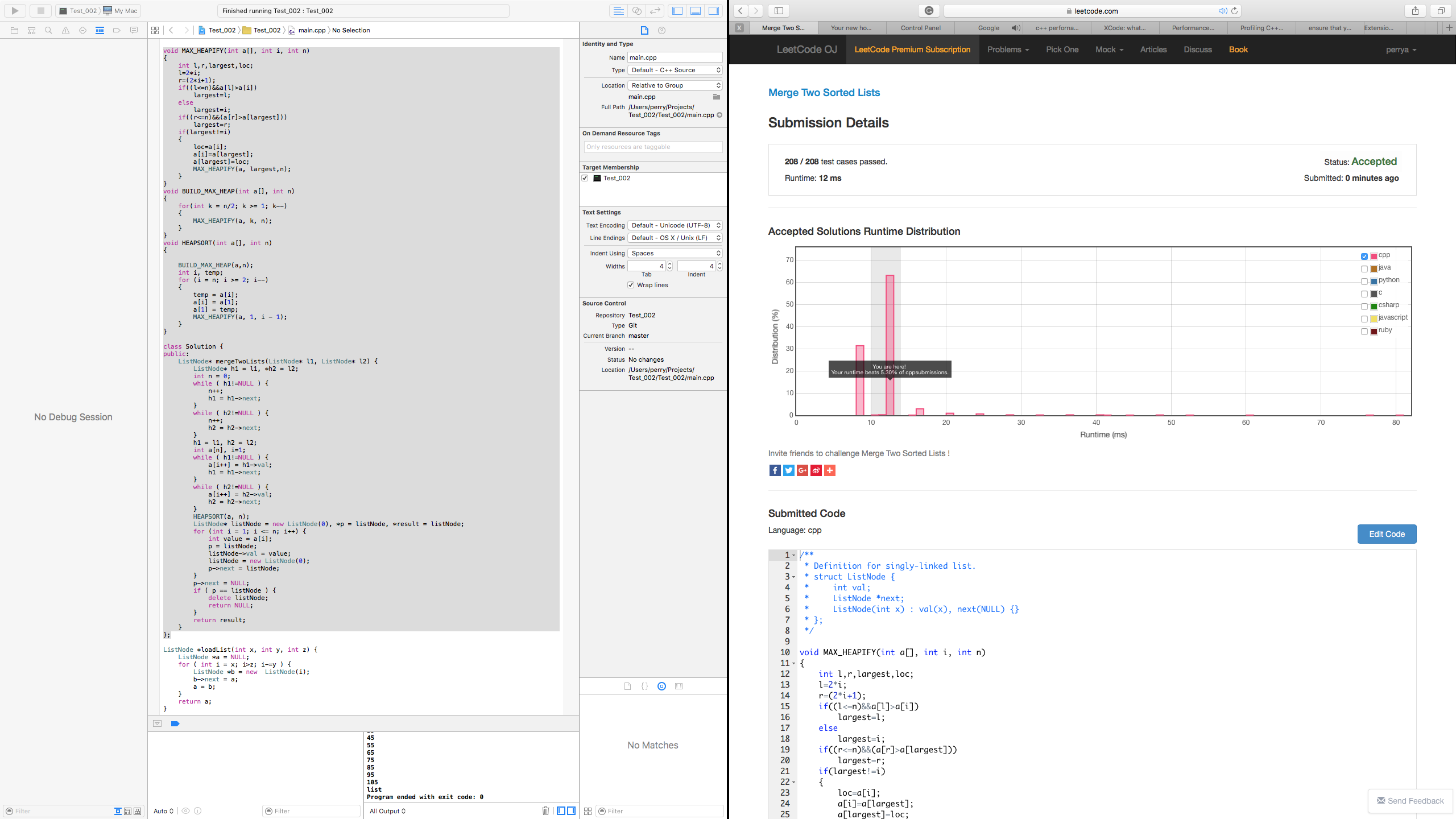
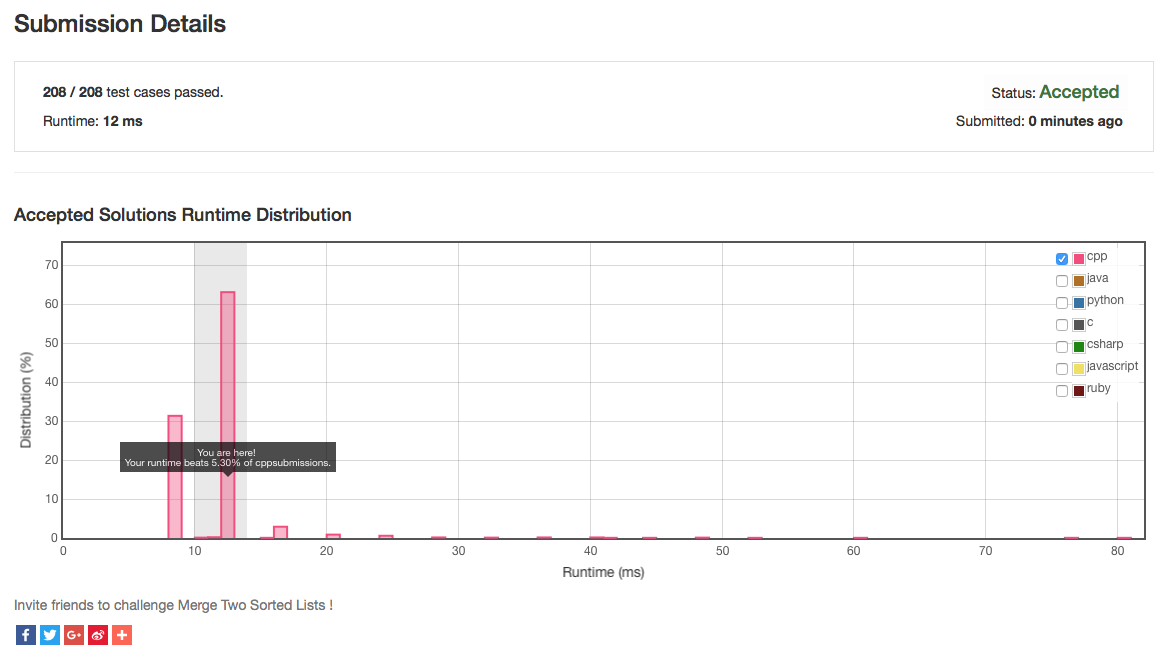
Here I borrowed a readily available implementation of a typical heap sort compliments a Avi Dhall on coders-hub.com. To get the int values from the link lists I have to add additional code to first figure out how long both lists are, then create an int array to hold all the int values. With this information I merely call the heap sort out of the box and then place the sorted array into a brand new link list to be passed back to the client.

What amazed me however is that the benchmarks provided by LeetCode OJ were practically identical to the original STL solution.

Right-click and "Save Image as ..." to get a better look at this image!

Thinking that perhaps I wasn't using the most efficient sorting algorithm I quickly tracked down a quick sort solution and made the appropriate changes. My justification for going through this trouble is that there remained a possibility that my solution was being tested against an extensive test suite where such issues as sorting algorithms would play a major role in the outcome of the solutions performance. For example in testing I am using a mere 10 ints each in two linked lists. But how would this solution perform if we had perhaps 100,000 ints or even a million ints to compare. I made the assumption that the test suite may be testing my solution against such a situation.

Solution #3: Classic Quick Sort Solution, Immutable parameters

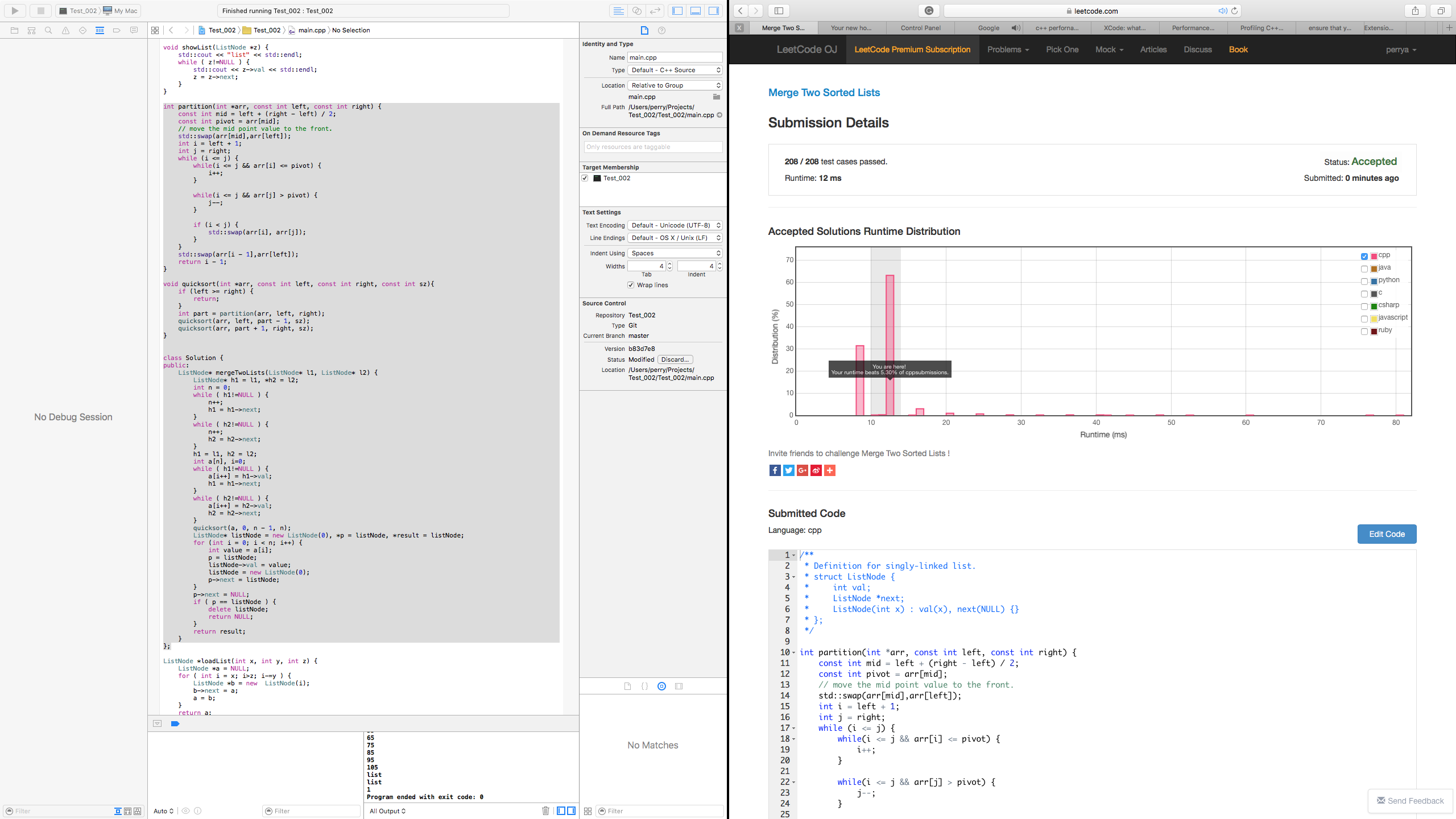
The following image is a snap shot of the 3rd solution developed and the results given by LeetCode OJ:

Right-click and "Save Image as ..." to get a better look at this image!

My third solution to this problem was a simple exchange of sorting algorithms however finding a quick sort algorithm online that was properly tested took a few attempts as the LeetCode OJ test suite kept spitting out subtle problems with a couple test cases. Again this is a none-STL solution applying a classic quick sort solution based on arrays:

// Solution #3

int partition(int *arr, const int left, const int right) {

const int mid = left + (right - left) / 2;

const int pivot = arr[mid];

// move the mid point value to the front.

std::swap(arr[mid],arr[left]);

int i = left + 1;

int j = right;

while (i <= j) {

while(i <= j && arr[i] <= pivot) {

i++;

}

while(i <= j && arr[j] > pivot) {

j--;

}

if (i < j) {

std::swap(arr[i], arr[j]);

}

std::swap(arr[i - 1],arr[left]);

return i - 1;

}

void quicksort(int *arr, const int left, const int right, const int sz){

if (left >= right) {

return;

}

int part = partition(arr, left, right);

quicksort(arr, left, part - 1, sz);

quicksort(arr, part + 1, right, sz);

}

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

ListNode* h1 = l1, *h2 = l2;

int n = 0;

while ( h1!=NULL ) {

n++;

h1 = h1->next;

}

while ( h2!=NULL ) {

n++;

h2 = h2->next;

}

h1 = l1, h2 = l2;

int a[n], i=0;

while ( h1!=NULL ) {

a[i++] = h1->val;

h1 = h1->next;

}

while ( h2!=NULL ) {

a[i++] = h2->val;

h2 = h2->next;

}

quicksort(a, 0, n - 1, n);

ListNode* listNode = new ListNode(0), *p = listNode, *result = listNode;

for (int i = 0; i < n; i++) {

int value = a[i];

p = listNode;

listNode->val = value;

listNode = new ListNode(0);

p->next = listNode;

}

p->next = NULL;

if ( p == listNode ) {

delete listNode;

return NULL;

}

return result;

}

};

Here I borrowed a readily available implementation of a typical heap sort compliments ROLFL on StackExchange. To get the int values from the link lists I have to add additional code to first figure out how long both lists are, then create an int array to hold all the int values. With this information I merely call the heap sort out of the box and then place the sorted array into a brand new link list to be passed back to the client.

Despite utilizing a different, more efficient sorting algorithm however there was almost no change in the performance reported by LeetCode OJ:

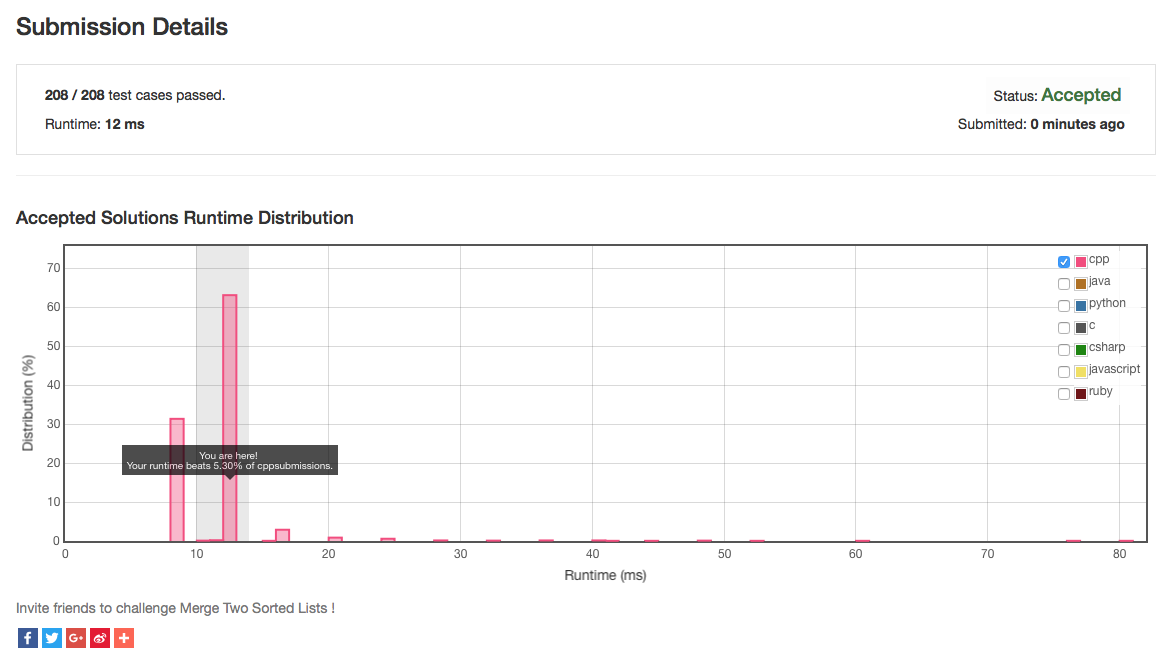
Right-click and "Save Image as ..." to get a better look at this image!

So this led me to believe that perhaps it was a memory utilization issue. That perhaps by eliminating the need to create a new link list I might be able to expedite the execution of the code. Essentially, what I would do is simply connect and reload the link lists passed as parameters with the sorted results as oppose to creating a third linked list.

Solution #4: Classic STL Solution, Mutable parameters

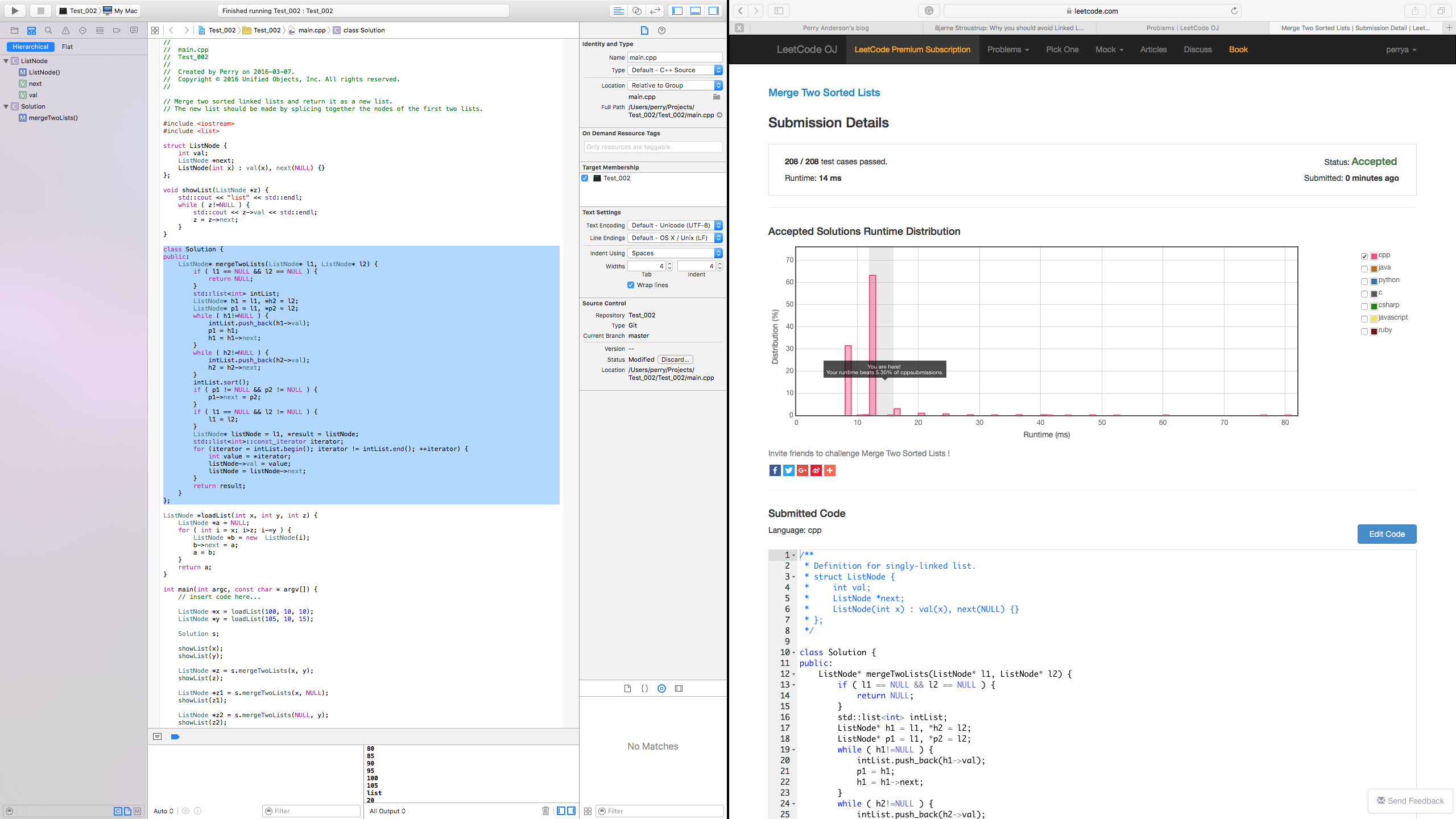
The following image is a snap shot of the 4th solution developed and the results given by LeetCode OJ:

Right-click and "Save Image as ..." to get a better look at this image!

My forth solution was a step back to the original STL solution (#1) however this time rather than creating a third link list, I'd simply connect the two linked lists passed as arguments then reload the link lists with the sorted int values. Constructing the code for this technique was a bit tricky and took longer than expected due to the many variable dancing around the code. However with Xcode's debugging facilities I was able to track down the correct variables for the correct purposes in time.

// Solution #4 (optimized)

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

if ( l1 == NULL && l2 == NULL ) {

return NULL;

}

std::list<int> intList;

ListNode* h1 = l1, *h2 = l2;

ListNode* p1 = l1, *p2 = l2;

while ( h1!=NULL ) {

intList.push_back(h1->val);

p1 = h1;

h1 = h1->next;

}

while ( h2!=NULL ) {

intList.push_back(h2->val);

h2 = h2->next;

}

intList.sort();

if ( p1 != NULL && p2 != NULL ) {

p1->next = p2;

}

if ( l1 == NULL && l2 != NULL ) {

l1 = l2;

}

ListNode* listNode = l1, *result = listNode;

std::list<int>::const_iterator iterator;

for (iterator = intList.begin(); iterator != intList.end(); ++iterator) {

int value = *iterator;

listNode->val = value;

listNode = listNode->next;

}

return result;

}

};

The result was a much shorter solution albeit a lot of concentration necessary to coordinate all the variables required. Further, this design kind of violates a cleaner coding practise of mine not to change the parameters which is what I am doing here. In the old C programming days it was much more common to change values inside the parameters that were passed to a function, with the introduction of more modern object-oriented tools like C++ and Java this practice became somewhat shunned except under exceptional circumstances. Essentially a function should begin at the top and exit at the bottom. Changing the solution to utilize the linked lists already in memory, while eliminating the need for allocating a new linked list, breaks this design convention. However, if ever we were faced with memory limitation issues this solution would work, where as the other solution would not.

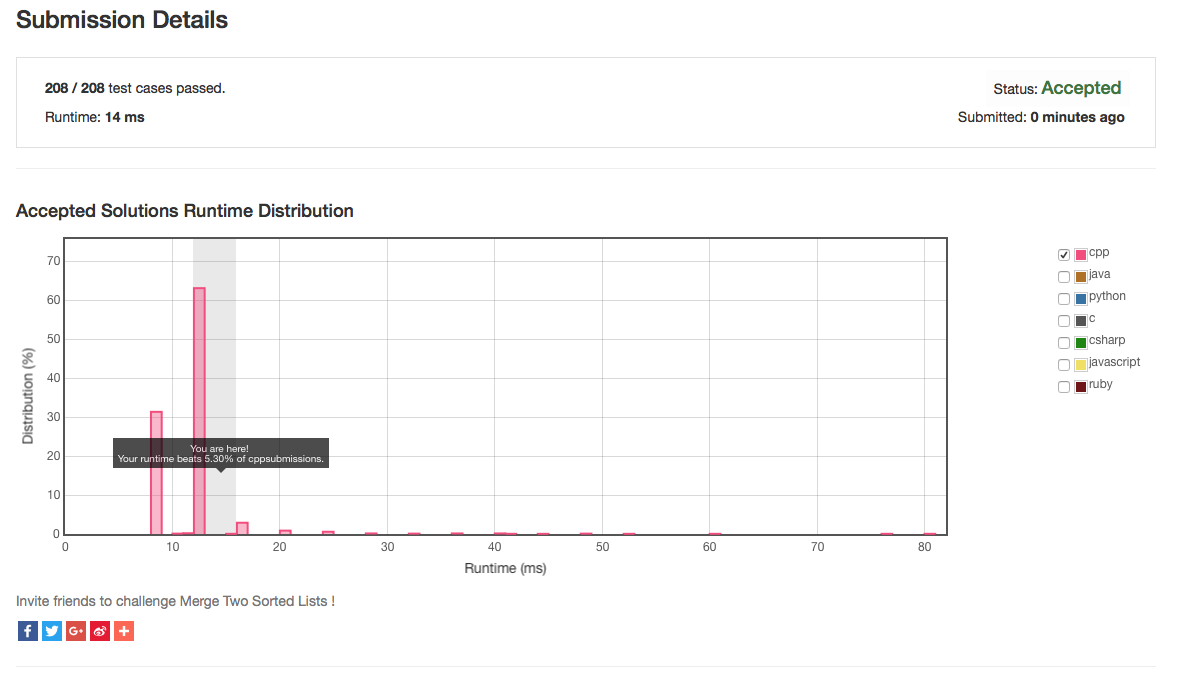
Right-click and "Save Image as ..." to get a better look at this image!

Despite the work I put into making these changes however, the resulting solution was reported to actually work slower, that is, according to LeetCode OJ's benchmarks. At the time I tested this solution however, I didn't realize I may have been reading the benchmark chart incorrectly. However, the fact that this benchmark had a very low red bar suggested to me that it had utilized far less memory resources as I had earlier. But I couldn't understand why this solution wasn't faster than before. So after some thought I decided to again try this approach albeit without utilizing the STL library.

Solution #5: Classic Quick Sort Solution, Mutable parameters

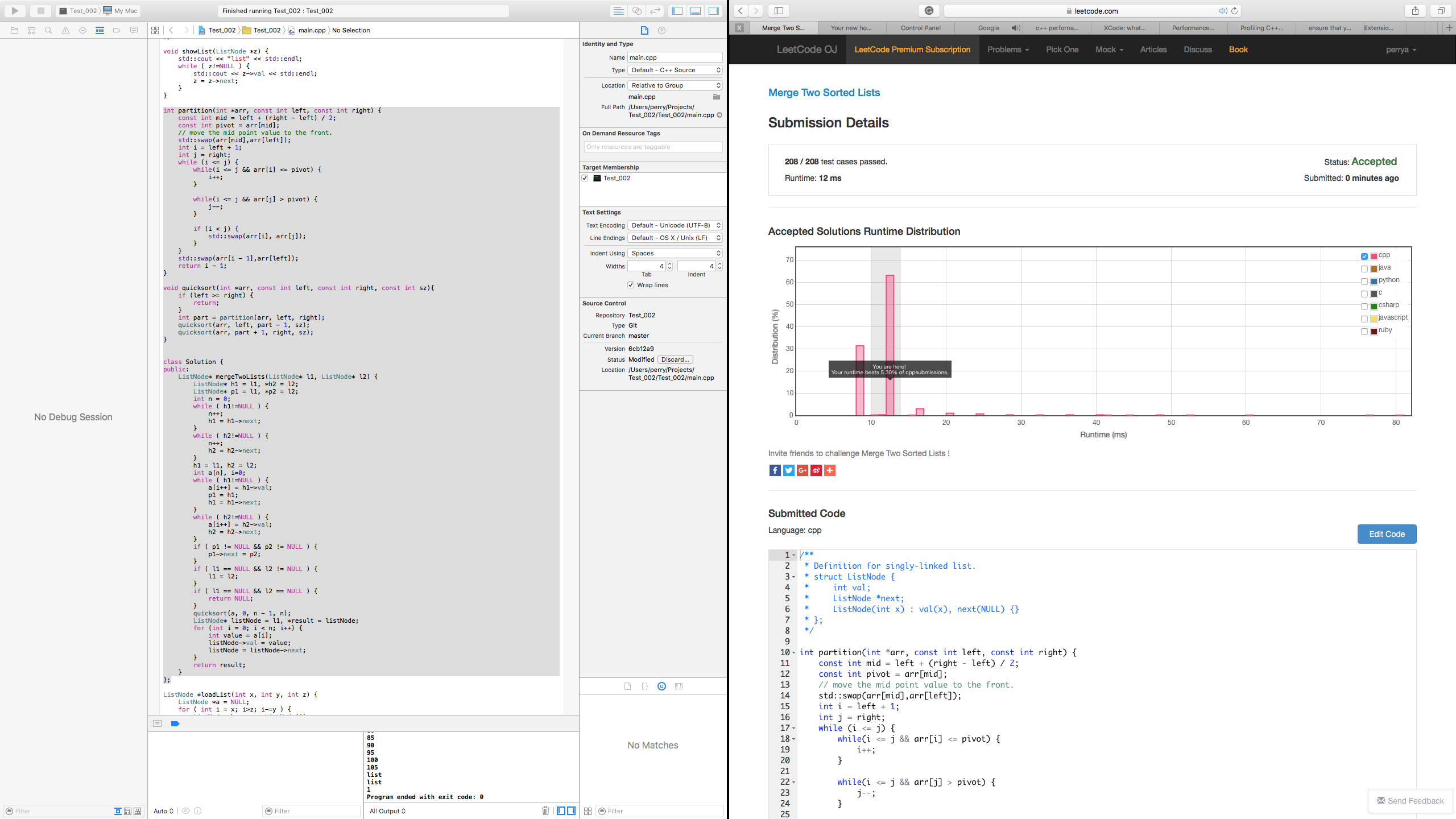
The following image is a snap shot of the 5th solution developed and the results given by LeetCode OJ:

Right-click and "Save Image as ..." to get a better look at this image!

My fifth solution was a step back to the quick sort solution (#3) . It is essentially the same as the forth solution except I am using arrays instead of the STL. I didn't have to trouble shoot this one as much as the forth solution, just carefully replace the STL functionality with a more generic approach using only arrays and the classic quick sort.

// Solution #5

int partition(int *arr, const int left, const int right) {

const int mid = left + (right - left) / 2;

const int pivot = arr[mid];

// move the mid point value to the front.

std::swap(arr[mid],arr[left]);

int i = left + 1;

int j = right;

while (i <= j) {

while(i <= j && arr[i] <= pivot) {

i++;

}

while(i <= j && arr[j] > pivot) {

j--;

}

if (i < j) {

std::swap(arr[i], arr[j]);

}

std::swap(arr[i - 1],arr[left]);

return i - 1;

}

void quicksort(int *arr, const int left, const int right, const int sz){

if (left >= right) {

return;

}

int part = partition(arr, left, right);

quicksort(arr, left, part - 1, sz);

quicksort(arr, part + 1, right, sz);

}

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

ListNode* h1 = l1, *h2 = l2;

ListNode* p1 = l1, *p2 = l2;

int n = 0;

while ( h1!=NULL ) {

n++;

h1 = h1->next;

}

while ( h2!=NULL ) {

n++;

h2 = h2->next;

}

h1 = l1, h2 = l2;

int a[n], i=0;

while ( h1!=NULL ) {

a[i++] = h1->val;

p1 = h1;

h1 = h1->next;

}

while ( h2!=NULL ) {

a[i++] = h2->val;

h2 = h2->next;

}

if ( p1 != NULL && p2 != NULL ) {

p1->next = p2;

}

if ( l1 == NULL && l2 != NULL ) {

l1 = l2;

}

if ( l1 == NULL && l2 == NULL ) {

return NULL;

}

quicksort(a, 0, n - 1, n);

ListNode* listNode = l1, *result = listNode;

for (int i = 0; i < n; i++) {

int value = a[i];

listNode->val = value;

listNode = listNode->next;

}

return result;

}

};

Essentially this solution manually tracks down the number of items in each list then creates an int array on the heap to store them for sorting. It also meticulously figures out where the end of the first list is and then connects to the start of the second list. It then sorts the ints and reloads them into the first list which is now both lists connected.

Right-click and "Save Image as ..." to get a better look at this image!

This approach eliminates the need to allocate memory for a third link list or the need to delete the first two link lists. Which is great from a memory allocation standpoint which I thought would make all the difference as far as performance was concerned. The only real change in performance was that now the LeetCode OJ graph showed the same performance as before. This quick sort, non-STL solution seemed to be better but at this point I was beginning to doubt the accuracy of the performance data presented by LeetCode OJ.

Solution #6: Classic Heap Sort Solution, Mutable parameters

The following image is a snap shot of the 6th solution developed and the results given by LeetCode OJ:

Right-click and "Save Image as ..." to get a better look at this image!

My sixth solution was a step back to the heap sort solution (#2) . It is essentially the same as the forth solution except I am using arrays instead of the STL. I didn't have to trouble shoot this one as much as the forth solution, just carefully replace the STL functionality with a more generic approach using only arrays and the classic heap sort. I did this for argument sake just to see if there was any performance differences being detected by the LeetCode OJ test suite.

// Solution #6

void MAX_HEAPIFY(int a[], int i, int n)

{

int l,r,largest,loc;

l=2*i;

r=(2*i+1);

if((l<=n)&&a[l]>a[i])

largest=l;

else

largest=i;

if((r<=n)&&(a[r]>a[largest]))

largest=r;

if(largest!=i)

{

loc=a[i];

a[i]=a[largest];

a[largest]=loc;

MAX_HEAPIFY(a, largest,n);

}

void BUILD_MAX_HEAP(int a[], int n)

{

for(int k = n/2; k >= 1; k--)

{

MAX_HEAPIFY(a, k, n);

}

void HEAPSORT(int a[], int n)

{

BUILD_MAX_HEAP(a,n);

int i, temp;

for (i = n; i >= 2; i--)

{

temp = a[i];

a[i] = a[1];

a[1] = temp;

MAX_HEAPIFY(a, 1, i - 1);

}

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

ListNode* h1 = l1, *h2 = l2;

ListNode* p1 = l1, *p2 = l2;

int n = 0;

while ( h1!=NULL ) {

n++;

h1 = h1->next;

}

while ( h2!=NULL ) {

n++;

h2 = h2->next;

}

h1 = l1, h2 = l2;

int a[n], i=1;

while ( h1!=NULL ) {

a[i++] = h1->val;

p1 = h1;

h1 = h1->next;

}

while ( h2!=NULL ) {

a[i++] = h2->val;

h2 = h2->next;

}

if ( p1 != NULL && p2 != NULL ) {

p1->next = p2;

}

if ( l1 == NULL && l2 != NULL ) {

l1 = l2;

}

if ( l1 == NULL && l2 == NULL ) {

return NULL;

}

HEAPSORT(a, n);

ListNode* listNode = l1, *result = listNode;

for (int i = 1; i <= n; i++) {

int value = a[i];

listNode->val = value;

listNode = listNode->next;

}

return result;

}

};

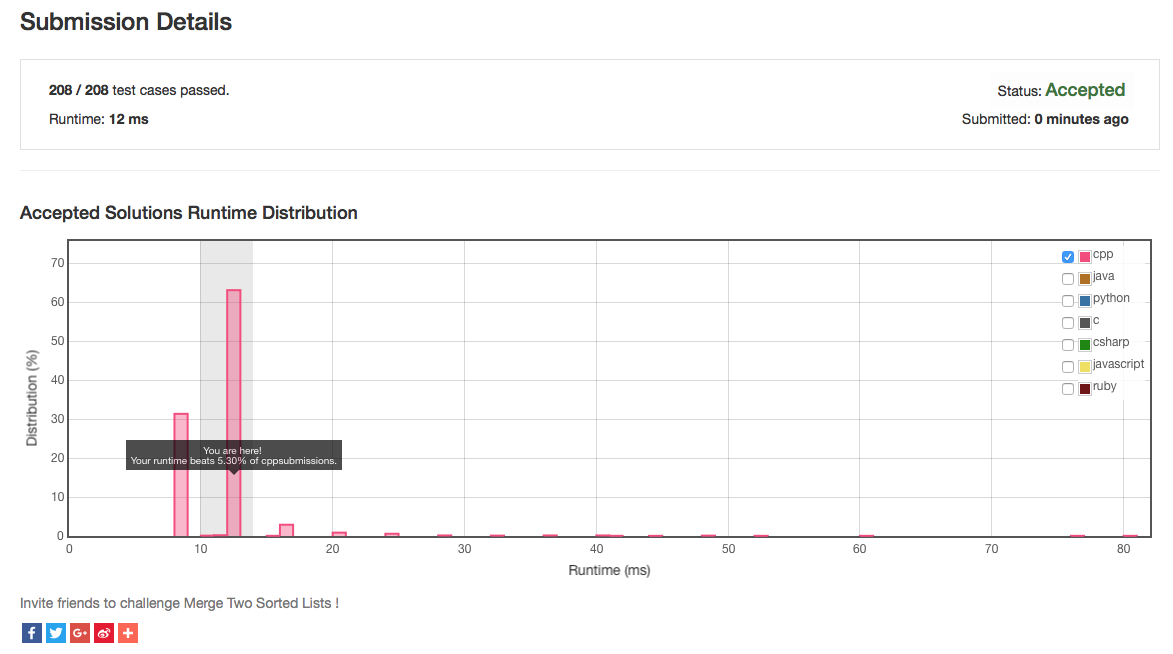
The resulting graph from LeetCode OJ showed no difference in performance:

Right-click and "Save Image as ..." to get a better look at this image!

It was at this point that I began to realize that the original STL solution worked just fine!

Further that the message "Your runtime beats 5.30% of cpp submissions." was misleading. In fact, a closer inspection of the graph provided by LeetCode OJ showed my solution in the top 94.7% bracket of posted solutions. It appears the graph was not entirely accurate based on the number of submissions, it was probably in err. For example, the graph goes from left to right where as the left of the graph indicates time of execution. My based on the 5.30% it was giving me, it suggested a lot of room for improvement when in effect, my solution was already in the top ten percent of submissions.

Solution #7: Intergrated STL/Quick Sort Solution, Mutable parameters

Before I realized I had been misinterpreting the LeetCode OJ data, I was giving serious thought to a possible 7th solution. One where I would combine the Quick Sort algorithm with both link lists in it's sorting process. Where I would simply change the values inside the link list nodes in the middle of the quick sort process. This of course I realize now would have been over kill but based on the data being presented to me I was so curious as to how everybody else seemed to be flying passed my solutions. Such a solution however would eliminate the need for maintaining a buffer of int values on the heap. If the link lists happen to contain millions of ints a solution such as this would be mandatory.

Synopsis:

The long and short of this excursion shows that the STL library was not only the first solution to meet this challenge but also the most elegant:

// Solution #1

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

std::list<int> intList;

ListNode* h1 = l1, *h2 = l2;

while ( h1!=NULL ) {

intList.push_back(h1->val);

h1 = h1->next;

}

while ( h2!=NULL ) {

intList.push_back(h2->val);

h2 = h2->next;

}

ListNode* listNode = new ListNode(0), *p = listNode, *result = listNode;

intList.sort();

std::list<int>::const_iterator iterator;

for (iterator = intList.begin(); iterator != intList.end(); ++iterator) {

int value = *iterator;

p = listNode;

listNode->val = value;

listNode = new ListNode(0);

p->next = listNode;

}

p->next = NULL;

if ( p == listNode ) {

delete listNode;

return NULL;

}

return result;

}

};

Anyone familiar with STL can easily recognize the solution provided hence it's maintainability is quite good. The only draw back on this solution has to do with environments where memory might be an issue. If for some reason we had an additional requirement where memory was limited then this alternative version using the same link lists passed in as parameters and linked together would work much better! However, there is a limitation even on this solution in the case of millions of link list entries. As the ints being sorted are being placed on the heap, hence only a raw link list solution (see below) which would not need a large heap would be required.

// Solution #4 ( aka. Solution #1 version 2 )

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

if ( l1 == NULL && l2 == NULL ) {

return NULL;

}

std::list<int> intList;

ListNode* h1 = l1, *h2 = l2;

ListNode* p1 = l1, *p2 = l2;

while ( h1!=NULL ) {

intList.push_back(h1->val);

p1 = h1;

h1 = h1->next;

}

while ( h2!=NULL ) {

intList.push_back(h2->val);

h2 = h2->next;

}

intList.sort();

if ( p1 != NULL && p2 != NULL ) {

p1->next = p2;

}

if ( l1 == NULL && l2 != NULL ) {

l1 = l2;

}

ListNode* listNode = l1, *result = listNode;

std::list<int>::const_iterator iterator;

for (iterator = intList.begin(); iterator != intList.end(); ++iterator) {

int value = *iterator;

listNode->val = value;

listNode = listNode->next;

}

return result;

}

};

Further, this entire presentation has been based upon the assumption that the link lists are not sorted in the first place. Had they been sorted a more straightforward solution based merely on attaching both linked lists by way of iterating through them would be fine. If both lists are already sorted before hand then is problem becomes merely a text book example of how to manage link lists. The solution you see below is not fully tested but it has the general idea of how a solution for this problem would take place in the case of both lists sorted ahead of time. And what you see below you is the idea solution as no memory management issues are required as you as simply rewiring a link list already in memory, assuming mutable parameters.

Word to the wise: Know when to say when!
Design by Contract is a popular concept among Eiffel programmers, essentially you determine ahead of time what a function has to do and you ensure that the function to be written only does what is expected. This includes checking the parameters for correct values before any processing takes place. The lesson to be gleaned from Design by Contract in my humble opinion is that get things done faster but making things simpler on yourself. Technically speaking, even though I didn't use a pure link list solution to this problem, by way of the STL I met the specification and delivered a working solution within an hour of the task at hand.

Merge two sorted linked lists and return it as a new list.

The new list should be made by splicing together the nodes of the first two lists.

The second version of Solution #1 meets both these requirements. Technically, by way of the STL framework, I have met the specification of this task. All in a days work!

The alternative method of piecing together a link list merge solution without the use of STL comparatively takes a lot longer given the many complications related to managing a link list. Based on what I read from Bjorne's ideals on why they developed the STL in the first place, I can easily appreciate today that if I had a boss that needed this done today there would be no contest, the STL solution gets things done. I say this out of experience. Quite often a boss needs a solution that works today and will quite often settle for an imperfect solution. It takes experience to know when to break down a problem in smaller parts to be delivered much more immediately as oppose to delaying progress while waiting for a more perfect solution.

Rational Unified Process
Also, to those of you familiar with the Rational Unified Process and it's Iteration Drive Development methodology, both solutions can compliment each other quite nicely. In other words, in a professional environment, if the situation called for memory and performance efficient solution for the long term, then a shorter term STL solution can be established first, then time given for a more specific solution for the long term if the situation demanded it.

Solution #8: Non-STL Merge solution assuming Two Sorted Lists

I am still so curious as to what LeetCode OJ considers 100%? When I find the time I will piece together a non-STL solution just to try to satisfy my curiosity. However, that being said, it generally takes a lot of time to piece together a solution like you see below and this demonstrates clearly how the use of the STL framework is a really great time saver. Hence, the original Solution #1 given in this presentation, while not the most memory efficient with respect to large case examples of millions of link list entries, is none the less far easily to implement and manage for smaller tasks that you generally see on a daily basis. Directly managing the internals of link lists are a hugely time consuming task, unless it is absolutely required due to exception circumstances, an out of the box STL solution is strongly recommended for most tasks. But for those of you who enjoy spending all day looking for needles in a haystack (which is what doing it without the use of STL is like) versus using a powerful magnet (which is what STL allows you to do) go for it. But after two hours of trying to piece together a none-STL solution to merging two sorted link lists without developing a complete set of proper test cases first, the solution presented earlier (See Solution #1 above) is strongly preferred and in fact far more practical.

// Solution #8 ( incomplete )

class Solution {

public:

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {

if ( l1==NULL && l2==NULL )

return NULL;

if ( l1==NULL && l2!=NULL )

return l2;

if ( l1!=NULL && l2==NULL )

return l1;

ListNode* result = l1;

if ( l2->val <= l1->val )

result = l2;

while ( l1!=NULL && l2!=NULL ) {

while ( l1!=NULL && l2!=NULL && l2->val <= l1->val ) {

while ( l2->next!=NULL && l2->next->val <= l1->val )

l2 = l2->next;

ListNode* a = l1->next;

ListNode* b = l2->next;

l2->next = l1;

if ( b!=NULL )

l1->next = b;

l1 = a;

l2 = b;

}

while ( l1!=NULL && l2!=NULL && l2->val > l1->val ) {

while ( l1->next!=NULL && l1->next->val < l2->val )

l1 = l1->next;

ListNode* a = l1->next;

ListNode* b = l2->next;

l1->next = l2;

if ( a!=NULL )

l1->next = a;

l1 = a;

l2 = b;

}

return result;

}

};

To go about developing a non-STL solution for this problem properly in a professional environment like Bloomberg, you'd want to develop a series of JUnit style test cases first. Which is essentially what the LeetCode OJ is providing in the background to run this solution against. This takes time and in some cases a considerable amount of time. It can be done of course but it's a bit like re-inventing the wheel. This is precisely the advantage of using STL. It takes all these standard data manipulating techniques and places them inside a template library for ease of reuse. In a world where getting things done fast and correctly is the order of the day, reinventing the wheel by tomorrow versus getting things done today is a choice few projects can go without! Unless there is something the STL is not already doing for you, your project leader is going to be a lot more satisfied with your work if you are using STL (imho). Furthermore, if your application depends on a lot of insertions and deletions then you'll find vector based solutions far more efficient than link lists due to fragmentation:

Why you should avoid Linked Lists, Bjarne Stroustrup
Day 1 Keynote, Bjarne Stroustrup: C++11 Style

What you have seen here is a typical day in software development for me. You utilize the tools you have available combined with what you understand as current and correct feedback. As for misunderstanding the task at hand "Merge Two Sorted Lists" it really doesn't matter as misunderstandings happen all the time. This is why we have the Rational Unified Process and Use Case driven development. In essence, the policy to make the time to take the time or vise-versa. To understand the customer better before any coding takes place as minor misunderstandings like this happen in life. However, the STL solution still solved both cases and did so within an hour, the only difference being that a pure non-STL solution might be more efficient. However, in real life, such efficiencies often come at the cost of time and money and in today's business world time is money. No where in the specification did the task at hand indicate that it had to be the fastest solution in the universe, hence I met the terms of the contract and saved my imaginary customer a tonne of money in consulting fees or lost production time. I was just curious as to why my solution wasn't considered near the top of the list as far as LeetCode OJ was concerned, hence the other versions of my solution. When time permits I will take the time to put in a proper non-STL version just to see if I hit a much higher rating. However I will also be noting just how long it took to put together said solution and compare the amount of time it took to re-invent the wheel verses my initial STL version which was completed within an hour of the task assignment. Had this been a real time engineering application, as is the case in my background in SCADA systems, this would have been a typical day at the office. To paraphrase the great Philippe Kahn: First you get it to work, then you get it to work better!

Thank you for taking the time to review this presentation.

PERRY ANDERSON: IT CONSULTANT PORTFOLIO